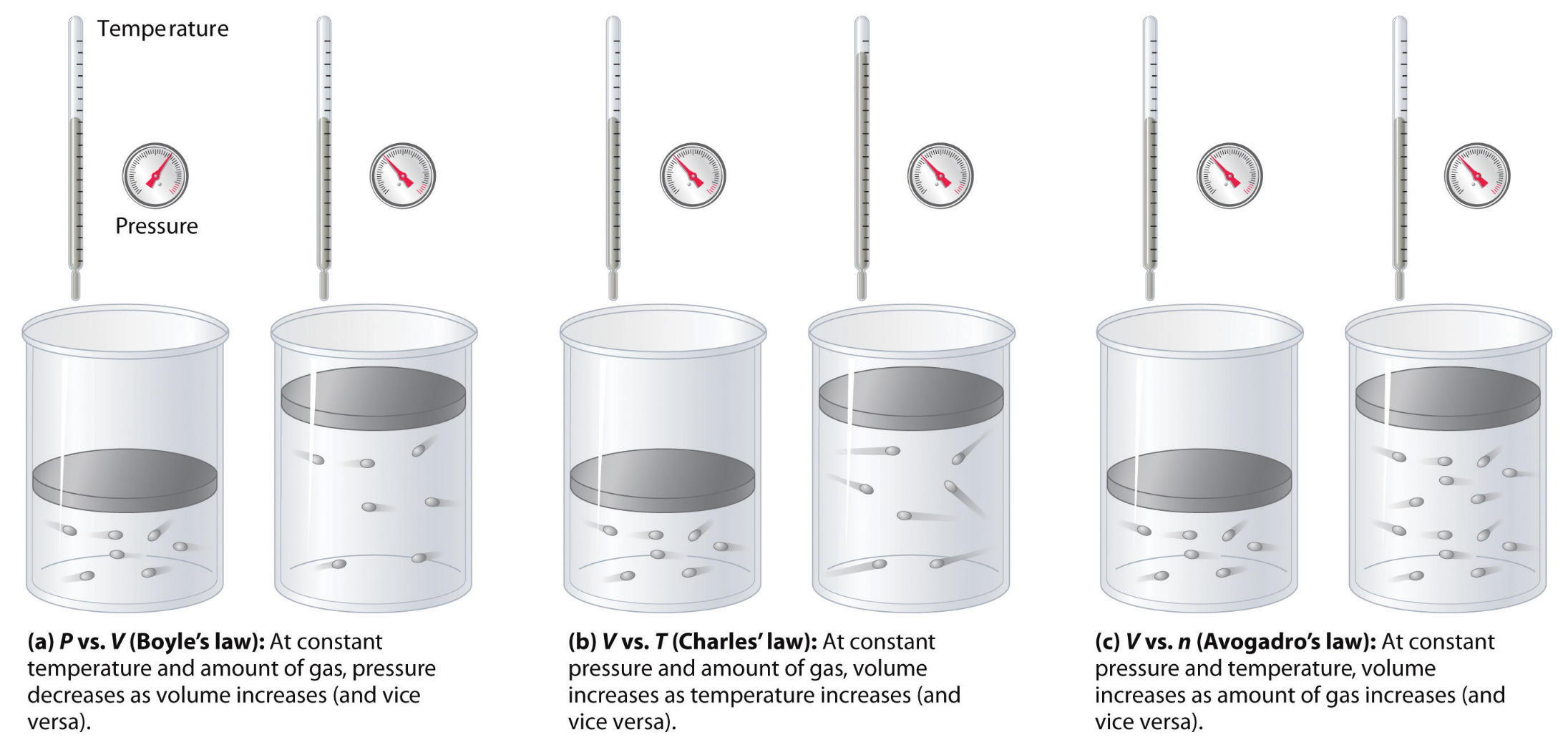
What we did in this unit was to re-develop three main gas theories using computational models and quantitative data analysis.

We defined the relationship between number of particles and pressure as:

• Qualitatively: As number of particles increases, pressure increases linearly (given that temperature and container volume are constant)
• Quantitatively: $(P)ressure = m_1 \times (N)umber$ , where $m_1$ is a constant coefficient.

We defined the relationship between gas temperature and pressure as:

• Qualitatively: As gas temperature increases, pressure increases linearly (given that number of particles and container volume are constant)
• Quantitatively: $P= m_2 \times (T)emperature$ , where $m_2$ is a constant coefficient.

And, we defined the relationship between container volume and pressure as:

• Qualitatively: As gas temperature increases, pressure increases linearly (given that number of particles and container volume are constant)
• Quantitatively: ${P} = {m_3 \over (V)olume}$ , where $m_3$ is a constant coefficient.

Our methodology and findings were analogous to three scientific discoveries made between 17^th and 19^th centuries:

However, as both the warning on the air duster can and the ballon-on-fire experiment showed, often times, we may not be able to explain gas-pressure related phenomena through just one variable. We need be combine our three theories and come up with one ideal gas theory. Let's try to do that!